《自然灾害》之地震灾害-03地震的特点
来源:陈颙, 史培军. 自然灾害[M]. 北京:北京师范大学出版社, 2007。
声明:版权归作者本人和北京师范大学出版社所有。转载请一定保留来源。
2 地震的特点
科学家们和公众询问地震的一个基本问题就是它的大小。表示地震大小基本有两种方法,一种是利用地震震级表示地震的大小;另一种是根据地震造成的破坏程确定地震的大小。
2.1地震的大小
地震作为一种自然现象,它有大有小,大可以大到使山崩地裂、房倒屋塌,小可以小到人体根本感觉不到、只有灵敏的仪器才能记录到。如何表示地震的大小呢?
第一种方法,用地震所释放的能量来表示地震的大小,用地震的震级(magnitude)表示地震所释放的能量的大小,震级大的地震,释放的能量就多。上面已经说过,地震所释放的能量可以用地震矩MO来表示。
M=μAD
其中μ是介质的剪切强度,A 是断层面的面积,D是断层两盘相互滑动的距离。用能量定义的震级叫做地震的矩震级MW。MW与地震矩MO的关系是:
MW = logMO/1.5 – a
式中a是一个常数,它与M0的单位选取有关,例如,金森博雄以牛顿·米作为M0的单位,a=6.06。若以达因·厘米(dyne-cm)为单位,则a=10.7。实际确定地震的震级时,根据地震仪记录到的地震波幅度的对数来进行标度的,这就是通常用到的里克特震级即里氏震级。
图26 几位著名地震学家1956年的合影,从左到右:Frank Press,Beno Gutenberg,Hugo Benioff和Charles Richter。其中里克特(Richter)是里氏震级的发明人。
来源 洛杉矶检查报
图27 根据地震仪记录到的地震波幅度确定地震的里氏震级
地震释放的地震波能量Es与震级M有下列关系(能量E以尔格计):
logE=11.8+1.5M
从上式可以看出,不同震级地震的能量差别是很大的。震级每大一级,地震的能量就大101.5(约31.6倍),即2级地震的能量是1级地震的31.6倍,3级地震的能量则是1级地震的101.5+1.5=1000倍。所以,尽管小地震数目比大地震多得多,但总能量中的大部分仍是由大地震释放的。
图28 自然界各种事件的能量排序
地震的能量到底处于什么数量级上呢?我们可以来做几个比较。如果把1945年美国扔在日本广岛的原子弹(相当于2万吨标准TNT炸药)埋在地下十几公里处让它爆炸,相当的震级是5.5级;而唐山地震则相当于2800颗这样的原子弹在地下爆炸。可见地震的能量是十分巨大的。我们还可以把自然界中的各种现象在能量上作一个排序。上图是以尔格表示的能量图。天上闪电的能量大概相当于1016尔格。现在已知最大的能量大约为1032尔格,这是7000万年前,一个直径10公里的天外星体以每秒20公里的速度撞到地球上,产生了大量的灰尘,使地球变成了一个黑暗的世界,有的学者认为正是这场灾难导致了恐龙的灭绝。这个能量是现在我们所知道的最大的。在这样一个广阔的能量图中,地震(图中的红点)大约位于其中部,例如唐山地震约相当于1023尔格。可见,地震作为地球上的一种自然现象,它的能量对于人类社会乃至整个自然界的影响都是相当大的。
图29 地震的震级和能量
地震的矩震级和里氏震级是表示地震大小的两种不同的震级,矩震级是上世纪80年代发展起来的,而里氏震级要早的多,是上世纪30年代提出的,因此,里氏震级应用要早.对于大多中等地震,两种震级基本相同,而对于特别大的地震,矩震级描述比里氏震级要好。
地震的几种不同的震级
里氏震级ML是里克特在1935年提出来的。它是以地震仪所记录到的地震波振幅为基础。当地震震源大小一定时,距离震源愈远震波的振幅就愈小;当与震源的距离一定时,则震波的振幅与震源的大小成正相关。
里氏震级被定义为︰一台标准地震仪(当时叫做伍德-安得生(Wood-Andersion)式地震仪,自由周期0.8秒,倍率2800倍,阻尼常数0.8),在距离震中100公里处所记录的最大振幅A(以微米计)的对数值︰
ML=log(A)
显然,100公里外发生地震,地震仪记录真实地动为1微米,则该地震为零级地震。同样,从里氏震级的定义可以知道,如果地震和台站之间距离不变,地震震级大1级,地震产生的震动的振幅大10倍;震级大2级,振幅大100倍;震级大3倍,振幅大1000倍,依次类推。
但是地震并非都发生在距离测站100公里处,因此在计算地震震级时,我们必须考虑震中距△(即震中与台站之间的距离, 以度为单位)的修正,则上式可以修正为︰
ML=log(A)+2.56log(△)-5.12
里克特还发现,上述里氏震级仅适用震中距离小于600公里的地震,当震中距离超过600公里时,用面波来确定震级比较适合。1966年苏黎士国际地震学会上进一步扩展了里氏震级,计算面波震级(Ms)时,应考虑最大振幅之外,还须考虑周期T和震中距离:
Ms=log(A/T)+1.66logΔ+3.3
里氏震级提出后约半个世纪,Kanamori发展出由地震矩(M0)计算地震的矩震级的方法(矩震级的测定正文中已有介绍)。这种发展基于两个原因。第一,里氏震级是一种测量震级,而矩震级则是考虑地震机理的物理震级;第二,里氏震级难以测量特大地震。当MW<7.25时,矩震级MW的测量结果与用里氏面波测量的震级MS的测量结果基本一致;但当MW> 7.25时,面波震级MS开始出现“饱和”,也就是测量出的面波震级MS低于能反映地震真实大小的矩震级MW。而当MW=8.0-8.5时,MS达到完全饱和,也就是此时无论MW如何增大,测量出的面波震级MS不再跟着增大。所以,当测定大地震的震级时,如果采用MW以外的其它震级标度,则会由于震级饱和而低估地震的震级。地震的矩震级对大地震无饱和的现象。
图30 几种震级的关系
表示地震大小的第二种方法,是用地震在地面上产生的破坏程度,地震越大,它产生的破坏就大。我们把地面及房屋等建筑物受地震破坏的程度叫做地震烈度。中国和世界上多数国家一样,采用12级的地震烈度表。下面给出不同地震烈度对应的地面破坏情况(习惯用罗马数字表示):
- 小于Ⅲ度:人无感受,只有仪器能记录到;
- Ⅲ度:夜深人静时人有感受;
- Ⅳ-Ⅴ度:睡觉的人惊醒,吊灯摆动;
- Ⅵ度:器皿倾倒、房屋轻微损坏;
- Ⅵ-Ⅶ度:房屋破坏,地面裂缝;
- Ⅷ-Ⅹ度:房倒屋塌,地面破坏严重;
- Ⅺ-Ⅻ度:毁灭性的破坏。
震级和烈度都是表示地震大小的量,但是两者有很大的不同.震级是表示地震所释放的能量的大小的,因此,一个地震只有一个震级。而烈度表示的是地面及房屋等建筑物受地震破坏的程度,对同一个地震,不同的地区,烈度大小是不一样的。距离震源近,破坏就大,烈度就高;距离震源远,破坏就小,烈度就低。还可以举个例子说明震级和烈度的不同,地震震级好象不同瓦数的日光灯,瓦数越高能量越大,震级越高。烈度好象屋子里受光亮的程度,对同一盏日光灯来说,距离日光灯的远近不同,各处受光的照射也不同,所以各地的烈度也不一样。
图31 烈度是地震造成地面及房屋等建筑物的破坏程度,它也是表示地震大小一种方法,地震越大,它产生的破坏就大,地震烈度就大。 但是,烈度和震级不同。一个地震只有一个震级。而烈度表示的是地面及房屋等建筑物受地震破坏的程度,对同一个地震,不同的地区,烈度大小是不一样的。距离震源近,破坏就大,震中处的烈度就高;距离震源远,破坏就小,烈度就低。图中I:烈度。M:地震震级;R:震中距。
图32 世界上几种常用的烈度表,大多数国家使用12级烈度表,最早的12级烈度表是由意大利科学家Mercalli在19世纪提出来的,判断烈度主要利用19世纪的建筑物的破坏情况。以后,根据20世纪末期建筑物的发展,修改了判断烈度的标志,新的12级烈度表被叫做修改后的Mercalli烈度表,简称MMI(Modified Mercallii Intensity)。中国使用的12级烈度表于MMI烈度表相近,烈度判断标志根据中国建筑的特色做了部分修改。
图33 唐山地震的震级为7.8级,它的烈度分布如上图所示:唐山X度;天津VII度;北京VI度。描述地震大小的两种方法可以通过地震震级和震中烈度联系起来:5级地震-震中烈度VI-VII度,6级地震-震中烈度VIII度;7级地震-震中烈度IX-X度;8级地震-震中烈度XI-XII度。
2.2 地震带
我们已经知道地震在地球上的分布不是完全没有规律的,也不是完全有规律的,即地震活动是规律性与随机性共存。从全球地震震中分布图上可以看出,地震主要分布在三个地震带上。首先约70%的地震分布在环太平洋地震带,包括日本、台湾、美国加州圣安德列斯断层区等著名的地震活动区。第二个地震带是从地中海到喜马拉雅的欧亚地震带,其上地震分布的特点是比较分散,不像环太平洋地震带那么集中那么有规则,欧亚地震带约占全球地震的15%左右。第三个地震带是沿着各大洋洋中脊分布的洋脊地震带,约占5%左右。全球地震的这种成带分布可以用板块学说来解释。板块学说认为,地球的岩石圈是由若干刚性块体组成的,板块内部相对比较稳定,各板块之间则发生俯冲、碰撞、剪切等多种作用,正是板块之间的相互运动造成了地震的孕育和发生,所以大多数地震都分布在板块的边缘地区。全球的地震基本上分布在这三个地震带上,但仍有约10%的地震不是那么有规律,而是分布在这些地震带之外、离板块边界相当远的地方。这就是所谓的“板内地震”,典型的如美国的新马德里地震带,它远离板块边界,却频繁发生大地震,中国大陆发生的地震多属“板内地震”,其发生机制仍然是个未解之谜。
图34 全球强震分布与板块构造
图35 中国地震台分布图(截止到2006年8月,共有:首都圈台网107个台,国家台网48个台,其他地区台网393个台。部分地震台资料可以在网上查到:www.csndmc.ac.cn)
中国现代地震仪器观测始于十九世纪末期。日本侵占台湾省后,在1897年建立了台北地震台,以后,又陆续建立了台南台(1898)、台中台(1902)、台东台(1902)、恒春台(1907)。1904年法国教会所属的上海徐家汇观象台增设了地震仪,建立了中国大陆第一个地震台。中国人自己建立的第一个地震台,是李善邦先生等1930年在北京建的鹫峰地震台,从1930年冬到1937年抗日战争爆发为止,共记录2472次地震。
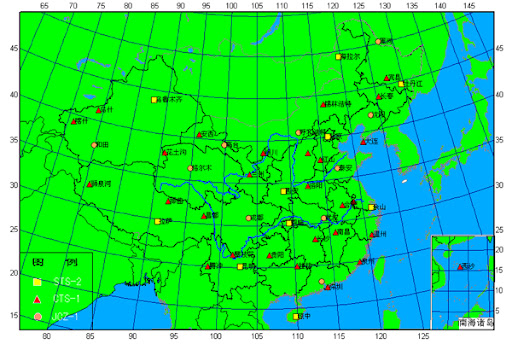
图36 中国地震震中分布图(公元前780年至2005年,地震的大小见图左下方的图标)
在中国的地震震中分布图上可以看到,震中分布有的地方密,有的地方稀,分布的规律远不如海洋地震那样有规律。这正是大陆地震与海洋地震不同的地方。按照地震分布的密集,同时,考虑到地质背景,也可以象海洋一样,划分出一些地震带来。例如,非常明显的一条南北地震带,它北起阿拉善地块,经山丹、民勤、银川与秦岭相遇,然后从天水,沿岷江上游而下,直至怒江、澜沧江,直到云南西部,全长2000多公里。又如,另一条是华北地震带,它始于西安附近,经华县,进入汾河河谷,再经临汾、太原、大同转而向东,过蔚县、怀来、延庆,直到渤海。中国大陆的地震震中分布比海洋要分散的多,这意味着,中小地震在大陆各地随机发生的可能性,比海洋要大的多。
图37 1900-2000年间中国大陆每年5级以上地震数目
2.3 地震的频度
根据位于伦敦的国际地震中心(ISC)的统计,从1964年开始到1999年,全球发生的各种大小的地震数目如下:
表1 国际地震中心ISC(1964-2001)地震数目统计
由于上世纪60年代之前,全世界的地震台站不多,许多小地震可能记录不到,所以国际地震中心(ISC)只给出1964年以后的结果。美国科学家恩达尔等统计了全世界各国的地震记录结果,发现:从1900年以来,7级地震的记录是完备的;1930年以来,6.5级地震的记录是完备的;1964年以来,5.5级地震的记录是完备的。下表是他们的统计结果:
表2 恩达尔等20世纪(1900-1999)目录统计
注:7级以上地震该记录是完备的,而7级以下地震则有许多遗漏。
以上的两种地震数目的统计,结果不尽相同,原因是所用的震级不同,ISC用的是里氏震级,而恩达尔等用的矩震级(如上个世纪,世界上记录到最大的地震是1960年发生在南美洲的智利地震,它的里氏震级为8.9级,而它的矩震级为9.5。对与多数地震而言,两种震级是比较接近的。),两种统计的时间段也不同。但他们的统计不仅让我们获得了地球上一年发生多少次地震的概念,而且还告诉我们关于大小地震之间的频度的关系。地震有大有小,那么到底是大的多还是小的多呢?从上面的表中可以看到,小地震比大地震要多,即震级越大、地震数目越少。实际上,这种多少是有一定比例关系的,即9级地震数目与8级地震数目的比值约等于8级与7级地震数目的比值,也约等于7级与6级地震的比值,这样可以依此类推下去。有趣的是,这种现象我们在自然界中遇到了很多,比如说,千年一遇的洪水与百年一遇的洪水数目的比值等于百年一遇的洪水与十年一遇数目的比值,还有天上的星星一等星与二等星数目的比值等于二等星与三等星的比值,等等,这些比值都是比例常数,都存在一个幂指数关系,这好像是自然现象的一个共同规律。而在地震学中这个现象发现得很早,这就是著名的古登堡─里克特关系(G-R关系),即若以N(M)表示震级大于M的地震数目,则N(M)与M之间有幂指数关系:
logN(M)=a-bM(其中a、b为常数)。从中可以容易推出N(M+1)/N(M)常数。
图38 美国地震信息中心(NEIC)给出的地震的大小和地震的数目的关系图。图中的颜色代表地震的震源深度。从图中可以看出,地震越大(震级越高),这种震级的地震数目越少。
图39 中国大陆1970年以来发生的震级大于或等于M的地震数据N(M)与地震震级M的关系:LgN=a-bM。其中a,b为常数:a=6.9,b=0.8

评论